Abstract
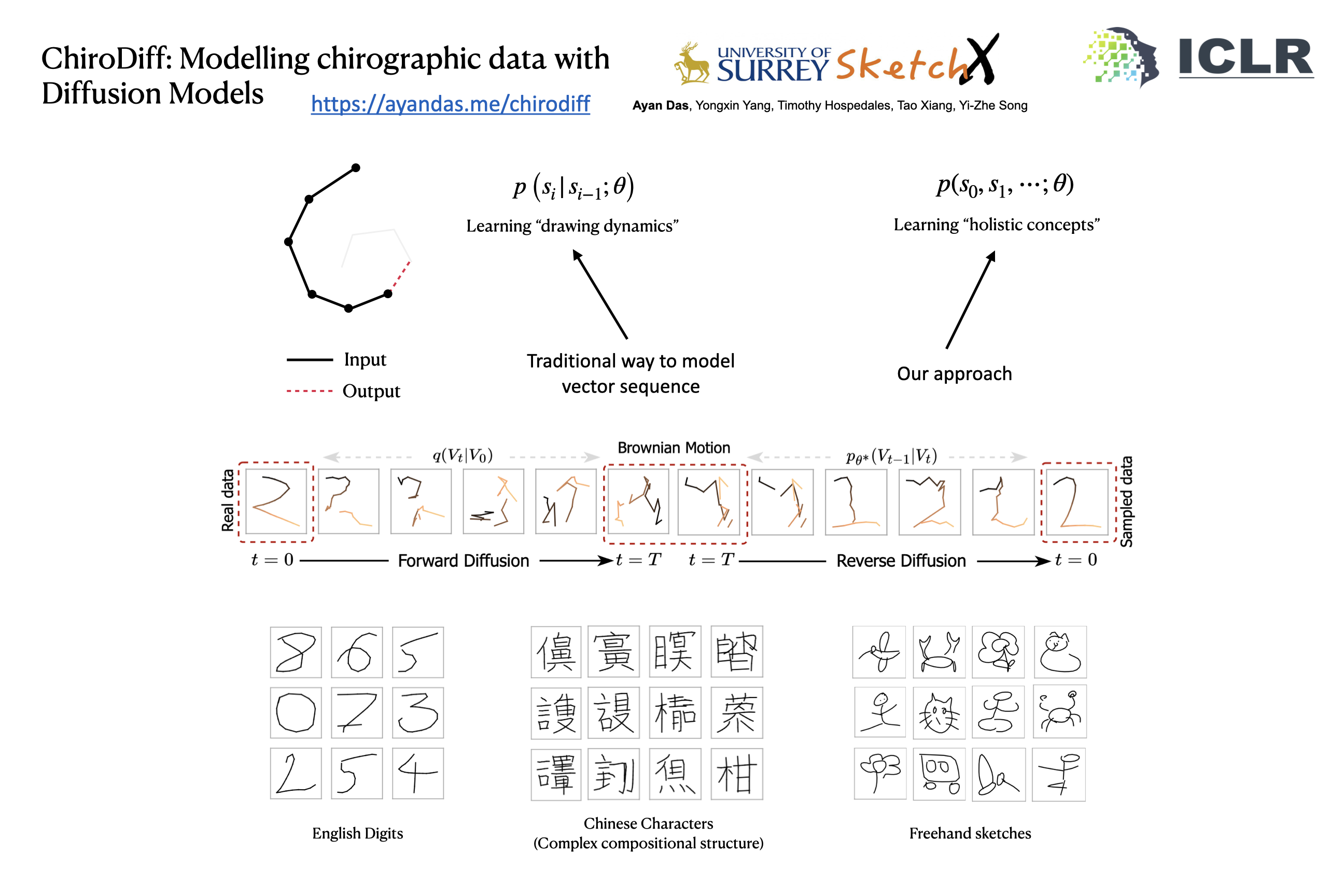
Generative modelling over continuous-time geometric constructs, a.k.a chirographic data such as handwriting, sketches, drawings etc., have been accomplished through autoregressive distributions. Such strictly-ordered discrete factorization however falls short of capturing key properties of chirographic data – it fails to build holistic understanding of the temporal concept due to one-way visibility (causality). Consequently, temporal data has been modelled as discrete token sequences of fixed sampling rate instead of capturing the true underlying concept. In this paper, we introduce a powerful model-class namely Denoising Diffusion Probabilistic Models or DDPMs for chirographic data that specifically addresses these flaws. Our model named ChiroDiff, being non-autoregressive, learns to capture holistic concepts and therefore remains resilient to higher temporal sampling rate up to a good extent. Moreover, we show that many important downstream utilities (e.g. conditional sampling, creative mixing) can be flexibly implemented using ChiroDiff. We further show some unique use-cases like stochastic vectorization, de-noising/healing, abstraction are also possible with this model-class. We perform quantitative and qualitative evaluation of our framework on relevant datasets and found it to be better or on par with competing approaches.
Citation
@inproceedings{das2023,
author = {Das, Ayan and Yang, Yongxin and Hospedales, Timothy and
Xiang, Tao and Song, Yi-Zhe},
title = {ChiroDiff: {Modelling} Chirographic Data with {Diffusion}
{Models}},
booktitle = {International Conference on Learning Representations
(ICLR), 2023},
date = {2023-01-21},
url = {https://openreview.net/pdf?id=1ROAstc9jv},
langid = {en}
}